day1总结

今天是国庆 xyd 集训的第一天。

模考

题目

T1

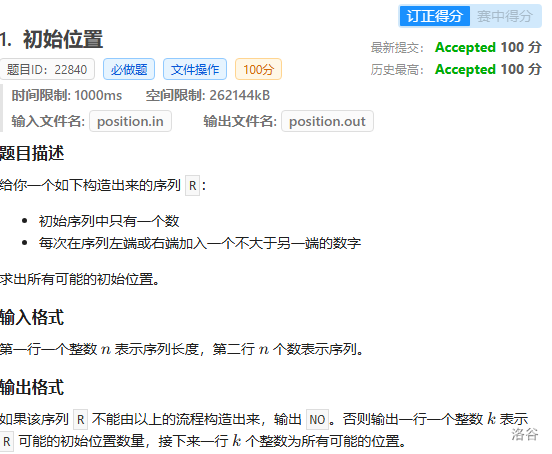
题意：指定一个空序列，在里面放入一个数字，能否通过每次在左右两端通过添加一个小于等于另一端的数字，形成一个数列 R。

一开考，就先看了 T1。

但是，应该是因为考试前比较赶，所以就在第一眼看 T1 的时候没有想到怎么写，就把问题想复杂了。

想成了要用二分。但是正解确是只需要对数组遍历之后取最大值，并用这个最大值尝试构造数组即可。

这题爆零应该是因为理解错了题意。

核心代码：

cin>>n;
for(int i=1;i<=n;i++){
    cin>>a[i];
    ans=max(ans, a[i]);
}
for(int i=1;i<=n;i++){
    if(a[i]==ans) cnt++;
}
cout<<cnt<<endl;
for(int i=1;i<=n;i++){
    if(a[i]==ans){
        cout<<i<<" ";
    }
}

T2

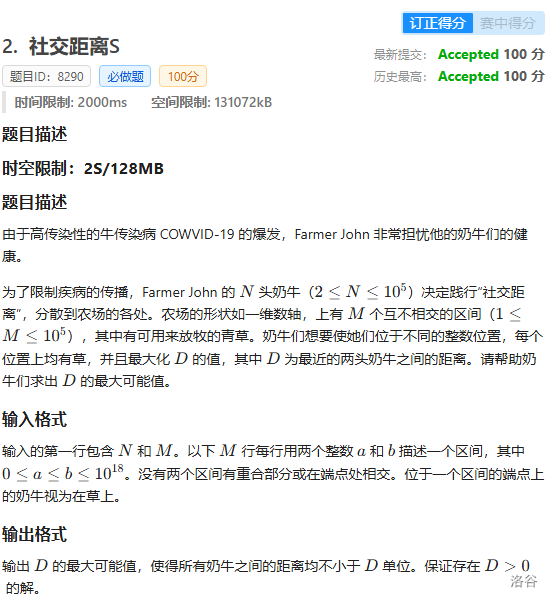
这题考试的时候 T1 在写完之后思路清晰了。

考试开始的时候还发现怎么 T2 没有文件读写，结果就是没有。

这题刚打开的时候感觉有思路了，但是写着写着突然发现了数据范围是到 $10^{18}$ 的，原本想要通过一个 bool 数组存下所有青草位置的想法瞬间被打乱 ，导致思路乱了，后面又思考了 20-30m，才思考出来。

思路其实就是二分答案，但是不知道为什么，我第一眼看到的时候就想着直接暴力枚举。。。

最后交之前验证了一下时间复杂度，算出来大概是 $O(m\ \log\ 10^{18})$，能过，就交上去了。

check函数：

bool check(ll d){
	ll cnt=0;
	ll last=-1e18-d;
	for(auto p:a){
		ll a=p.first;
		ll b=p.second;
		
		if(max(a,last+d)>b) continue;

		ll k=(b-max(a,last+d))/d;
		cnt+=k+1;
		
		last=max(a,last+d)+k*d;
		if(cnt>=n) return true;
	}
	return cnt>=n;
}

T3

T2 写完之后，我大概把 T3 和 T4 都看了一遍， 但是感觉还是T4更简单，就先写了 T4。

T4

T4 是一个图的问题，这里看一下就可以想到使用 BFS。

这个考试的时候其实一下子就看出来了。但是一开始没想到使用单独连接叶子结点的点这一方法，就写了从每个叶子节点（特殊点）出发，向内搜索。但是我写着写着，忽然想起来之前好像在哪里见过这种方法，便半路该了方法，使用了单独创建一个节点，连接所有叶子节点的方法，原理其实就是通过 BFS 的特性（？），就是遍历时会先扩展到每个与他相连的节点，而我们已经把这个单独节点连接到了每个叶子节点，就省去了要多次 BFS，特别是多次清空标记数组的麻烦（还是失分点）。

最后，还要记得在输出前排序一下。

核心代码：

vector<vector<int>> adj(n+1);
vector<int> de(n+1,0);
for(int i=0;i<n-1;i++){
    int u,v;
    cin>>u>>v;
    adj[u].push_back(v);
    adj[v].push_back(u);
    de[u]++;
    de[v]++;
}

vector<int> d(n+1,-1);
queue<int> q;
for(int i=1;i<=n;i++){
    if(de[i]==1){
        d[i]=0;
        q.push(i);
    }
}

while(!q.empty()){
    int u=q.front();
    q.pop();
    for(auto v:adj[u]){
        if(d[v]==-1){
            d[v]=d[u]+1;
            q.push(v);
        }
    }
}


int maxn=-1;
vector<int> ans;
for(int i=1;i<=n;i++){
    if(de[i]==1) continue;
    if(d[i]>maxn){
        maxn=d[i];
        ans.clear();
        ans.push_back(i);
    }
    else if(d[i]==maxn){
        ans.push_back(i);
    }
}